Ausgabe 22 · April 2016
Diesen Artikel als PDF
Deichselbruch an selbstgebautem Fahrradadanhänger: Analyse mit Bremskraftmessungen, Belastungsrechnungen und Finite-Elemente-Methode
von Eberhard und Lukas von Berg
Abstract
Beim Selbstbau eines Fahrradanhängers ist Aluminium der gebräuchliche Werkstoff. Für die sichere Auslegung der Anhängerdeichsel sind Abschätzungen der auftretenden Belastungen und der dadurch im Bauteil verursachten Spannungen erforderlich. Das wird am Beispiel der Überprüfung einer aus AlMgSi05 gefertigten Deichsel anhand des Lastfalls »Vollbremsung mit beladenem Hänger« dargestellt. Die Bremsverzögerung wird aus den Signalen eines Hallgebers am Hängerrad bestimmt. Die Bremskräfte werden mit einem in die Deichsel eingebauten Kraftaufnehmer ermittelt und durch ein einfaches Zweikörpermodell für Rad und Hänger bestätigt. Nach einer Vortestserie werden sieben Bremstests detailliert vermessen. Ein beim siebtenTest erfolgter Deichselbruch setzt dem Testen ein jähes Ende.
In der Analyse erweist sich die Federwirkung der verwendeten Kupplung als kritisch, weil dadurch ein Überschwingen der Bremskraft über den Gleichgewichtswert auftritt. Aus dem Biegemomentverlauf entlang der Deichsel wird die radseitige Biegung des Deichselrohrs als kritische Belastungsstelle identifiziert. Die dort auftretenden Spannungen werden durch analytische ein- und zweiachsige Spannungsberechnungen sowie durch FEM-Berechnungen ermittelt. Alle Rechnungen zeigen, dass die gewählte Auslegung der Deichsel hinsichtlich Wandstärke, Biegeradius und Werkstoffkennwerten nicht sicher ist. Aus den durchgeführten Parametervariationen lassen sich sichere Gestaltungsvarianten ableiten. Weiter werden nachträgliche Verbesserungsmöglichkeiten durch Aussteifung der Deichsel diskutiert.
1. Einleitung
Für Fahrradanhänger ist ein niedriges Eigengewicht von Vorteil, weshalb bei vielen kommerziellen Modellen Aluminium als Werkstoff für den Rahmen und Textilbespannungen für die Seitenwände verwendet werden. Daher wurde für den Eigenbau eines Fahrrad-Lastenanhängers, der dann in einem Sozialprojekt der Vinzenzgemeinschaft Graz in Kleinserie mehrfach angefertigt wurde, ebenfalls diese Bauweise gewählt. Die Anhängerdeichsel wurde dabei aufgrund einer groben, überschlägigen Auslegung aus einem Rohr mit 25 mm Außendurchmesser und 2 mm Wandstärke aus AlMgSi0,5 (EN AW-6060) angefertigt.
Wegen im Nachhinein aufgekommener Sicherheitsbedenken wurden die im folgenden dargestellten Bremstests durchgeführt, wobei die Deichsel bereits nach wenigen Tests brach. Daraufhin wurden Berechnungen zur Belastung beim Bremsen sowie den zu erwartenden maximalen Spannungen angestellt. Die Rechenergebnisse wurden mit der Streckgrenze und der Biegewechselfestigkeit verglichen, woraus hervorging, dass die gewählte Deichsel nicht betriebssicher ist. In der Folge wird ein möglicher Versagensmechanismus diskutiert und abschließend werden Verbesserungsvorschläge zur Erhöhung der Betriebssicherheit der Deichsel gegeben, die in eventuellen Folgeprojekten nützlich sein könnten, aber vielleicht auch für den einen oder anderen Anhänger-Selbstbauer von Interesse sind.
2. Messtechnik
Für die Bremstests wurde die Deichsel mit einer Wägezelle (Bosche S40S) zur Normalkraftmessung instrumentiert (Bild 1) und ein Hallgeber zur Ermittlung der Fahrgeschwindigkeit und der Beschleunigungen sowie des Fahrwegs am linken Anhängerrad angebracht.
Das Signal der Wägezelle wurde über einen Messverstärker (Bosche WTE) ebenso wie das Signal des Hall-Gebers an Analog-Eingänge eines Arduino-Mikroprozessors gesendet. Um ausreichend Daten während der Messfahrten speichern zu können, wurde der Arduino-Prozessor mit einem Speichershield ergänzt, auf den die Datensätze in Blöcken zu 50 Zeilen ausgeschrieben wurden. Durch die Technik des blockweisen Schreibens aus dem Arduino-Arbeitsspeicher konnte eine sehr hohe Datenrate mit einem Aufnahmeintervall von 3-5 ms erzielt werden, die allerdings regelmäßig nach etwa 200 … 250 ms von Schreibpausen von etwa 40 ms unterbrochen wurde.
Die komplette Elektronik samt Stromversorgung wurde in einer Stapelbox verpackt, auf dem Gepäckträger des Zugrads montiert und mit den Messleitungen von Hallgeber und Wägezelle verbunden (s. Bild 1 bis 5).
3. Testbedingungen
Der Hänger wurde mit einer Kiste Bier und einer PKW-Bremsscheibe aus der Schrottkiste beladen. Damit ergab sich eine Nutzlast von 30,6 kg, was circa 75 % der gewünschten Nenn-Nutzlast von 40 kg ausmacht. Der Hänger mit modifizierter Deichsel wog 13,8 kg, sodass sich ein Gesamtgewicht





von 44,4 kg ergab. Als Testrad wurde ein älteres Damenrad mit vor kurzem frisch montierten Bremsbelägen verwendet. Daher war zu erwarten, dass die nach der österreichischen Fahrradverordnung vorgeschriebene minimale Bremsverzögerung von a = 4 m/s2 erreicht werden kann. Eine Abschätzung zeigt, dass die Bremskraft F = ma ≈ 180 N beträgt und somit z.B. bei einer Bremsverzögerung a = 5 m/s2 etwa 220 N beträgt. Die Tests wurden auf einem ebenen Straßenstück von etwa 100 m Länge durchgeführt. Vor der Darstellung der Versuchsergebnisse sollen die zu erwartenden Kräfte beim Bremsvorgang mit einem einfachen Rechenmodell noch etwas genauer abgeschätzt werden.
4. Rechenmodell für den Abbremsvorgang
Um den Bremsvorgang rechnerisch zu beschreiben, wurde ein Zweikörper-Modell erstellt, das aus gebremster Zugradmasse und der mit einer Feder angekoppelten Hängermasse besteht. Die Steifigkeit der Kopplung wurde durch Hintereinanderschaltung der Deichselsteifigkeit und der Kupplungsfedersteifigkeit ermittelt. Weiter wurde eine zur Geschwindigkeit proportionale Dämpfungskraft angenommen.
Bild 6 zeigt das Zweikörper-Modell von Rad und Anhänger mit den angreifenden Kräften, wobei Index 1 das Rad und Index 2 den Anhänger bezeichnen, die jeweils die um die Deichsellänge l versetzen Koordinaten x1 und x2 besitzen. Die Massen werden mit m, die Kräfte mit F, die Federkonstante der Kopplung zwischen den Massen mit c, die Dämpfungskonstante mit d und die Geschwindigkeiten mit u bezeichnet. Das gebremste Rad wird als gleitender Körper idealisiert, die am Anhängerrad noch angreifenden Rollreibungskräfte werden als klein gegenüber der Bremskraft angesehen und deshalb vernachlässigt.
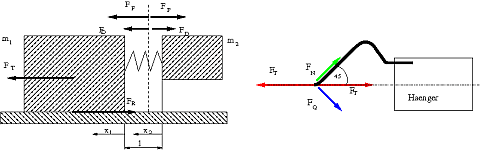
Es wurden die folgenden Modellgleichungen verwendet.
Zunächst gilt für das Gesamtsystem das Gleichgewicht aus Gesamt-Trägheitskraft FT und Reibungskraft FR, die gleich der mittleren Bremsverzögerung a mal der Gesamtmasse gesetzt werden kann.
Die Bewegungsgleichung für das Fahrrad erhält man, wenn man das System zwischen den Einzelmassen auftrennt und dafür als Schnittkräfte die Federkraft FF und die Dämpfungskraft FD anbringt. Am Fahrrad mit der Masse m1 steht dann die Trägheitskraft des Zugrades im Gleichgewicht mit der Bremsverzögerung sowie mit der Federkraft und der Dämpfungskraft der Kupplung, die parallel zur Federkraft angreifend angenommen wird.
Am Anhänger mit der Masse m2 wirken neben der Trägheitskraft des Anhängers noch die entsprechenden Schnittkräfte des Fahrrades.
Bei Bremsbeginn (t = 0 s) gelten die Startbedingungen:
wobei die Geschwindigkeit u0 beim Einleiten der Bremsung aus den unten dargestellten Messungen zu etwa 7 m/s bestimmt wurde. Setzt man
so erhält man das folgende Gleichungssystem,
das mit dem freien Matlab-Clone Octave gelöst wurde.
Mit einer angenommenen Masse von 90 kg für Rad und Fahrer und 44 kg für den Hänger sowie den unten diskutierten Steifigkeiten und Dämpfungskonstanten erhält man daraus die Geschwindigkeits- und Wegkurven von Rad und Hänger sowie die Deichselkraft und die Relativbewegung zwischen Rad und Hänger. Unsicherheiten bestehen bezüglich der Gesamtsteifigkeit c der Kopplung sowie der Dämpfungskonstante d, die aus Messungen bestimmt oder parametriert werden müssen. Die Steifigkeit der Kopplung zwischen den Massen lässt sich durch Hintereinanderschaltung der Deichselsteifigkeit cD und der Kupplungsfedersteifigkeit cF durch reziproke Mittelung bestimmen.

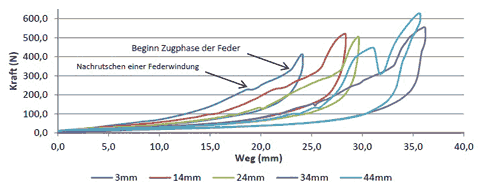
In einer von K. Huber 2013 an der TU Graz durchführten Bachelor-Arbeit [Huber 2013] werden für eine baugleiche Radanhängerdeichsel, die im eingangs genannten Sozialprojekt verwendet wurde (Beschäftigungsprojekt für arbeitslose Roma unter Trägerschaft der Vinzenzgemeinschaft Graz), Versuche zur Ermittlung der Deichselsteifigkeit beschrieben. Aus Druckversuchen wird darin ein Wert von cD = 53000 N/m für die Deichselsteifigkeit ermittelt und für die Kupplungsfeder (s. Bild 7) abhängig von der wirksamen Federlänge ein Diagramm angegeben, das eine progressive Federwirkung ab etwa 100 N Zugkraft zeigt (s. Bild 8). Die Feder wirkt dabei wegen der 45 Grad-Anlenkung vor allem als Biegefeder. Bis 100 N ergeben sich aus dem Diagramm z.B. bei 24 mm freier Federlänge, wie sie in den hier beschriebenen Tests vorlag, etwa 5.000 N/m, darüber im Bereich bis zu etwa 300 N Zugkraft steigt der Wert bis auf etwa 20.000 N/m.
Aus den Kraftmessungen der unten beschriebenen Bremstests kann man aus der Periode der auftretenden Kraftpeaks ebenfalls auf die Federkonstante c des gekoppelten Systems schließen. So ergeben sich dort z.B. aus Bild 14 aus den Kurven für Test B3 (lila) zwischen 5 und 10 s etwa 8 Schwingungen, was eine Schwingungsdauer von 0,625 s ergibt. Aus dem in Bild 15 sichtbaren Nachschwingen des Hängers nach Stillstand erhält man aus der Amplitudendifferenz aufeinander folgender Kraft-Peaks der Versuche B2 (gelb) bzw. B4 (schwarz) eine Periode der gedämpften Schwingung von etwa 0,72 s. Weiter kann man aus den Amplitudenabsenkungen der Kraftpeaks nach Stillstand, über das logarithmische Dekrement Λ = ln(27 N / 14 N) = 0,66 abgeschätzt, die Dämpfungskonstante d der Ankopplung ermitteln. Aus den Gleichungen für die Kreisfrequenz der gedämpften Schwingung
und der Definitionsgleichung des logarithmischen Dekrements Λ [Kurzweil 2009]
erhält man bei bekannter Schwingungsdauer Td und bekanntem Verhältnis zweier aufeinanderfolgender Kraftamplituden Fk und Fk+1 die Federkonstante c und die Dämpfungskonstante d zu
und
Kombiniert man die aus Druckversuchen in [Huber 2013] ermittelte Deichselsteifigkeit cD = 53.000 N/m mit einer Kupplungsfeder-Steifigkeit von cF = 5.000 N/m (ebenfalls nach [Huber 2013] ) so erhält man einen kombinierten Wert von etwa 4.570 N/m, was gut zu den aus den Kraftmessungen abgeleiteten Werten passt (siehe unten stehende Tabelle). Dieser Wert wurde daher in den Rechnungen mit dem Zweikörper-Modell verwendet. Dabei wurden jeweils Dämpfungswerte von 100 Ns/m (geringe Dämpfung) und 200 Ns/m (starke Dämpfung) eingesetzt (Gl. 11). Die innere Deichselsteifigkeit trägt genau genommen nicht zu den äußeren Kraftwirkungen auf die Deichsel bei, sie wird lediglich für die vereinfachte Betrachtung der Massenkopplung im Zweikörper-Modell benötigt. Die Steifigkeit der Deichsel ist aber gegenüber der Kupplungsfeder so groß, sodass man die Deichselsteifigkeit bei der hier vorliegenden Hintereinanderschaltung vernachlässigen kann.
| Fall |
T [s] |
Λ [-] |
cK [N/m] |
cD [N/m] |
c [N/m] |
d [Ns/m] |
|---|---|---|---|---|---|---|
| 1 | - | - | 5000 | 53000 | 4570 | - |
| 2 (aus Bremstests) | 0,72 | 0,66 | - | - | 3388 | 80 |
| 3 (aus Bremstests) | 0,63 | 0,66 | - | - | 4496 | 93 |
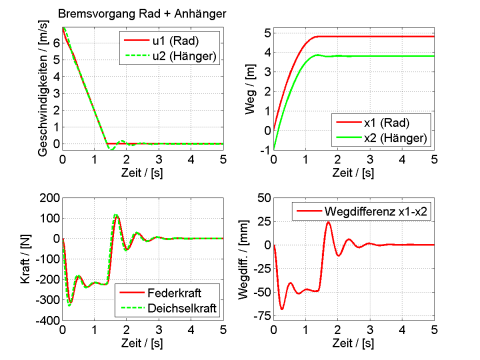
Bild 9 und 10 zeigen die zugehörigen Rechenergebnisse. Man erkennt als Hauptresultat aus diesen Bildern einerseits, dass sich die Bremskraft im Mittel auf den aus der Handabschätzung bestimmten Wert einschwingt. Andrerseits findet jedoch in beiden Fällen ein starkes Überschwingen statt, was kurzfristig deutlich höhere Kraftamplituden bewirken kann als via Handabschätzung berechnet wurde. Das weist bereits auf einen kritischen Bereich im Hängerbetrieb bei starken Bremsungen hin.
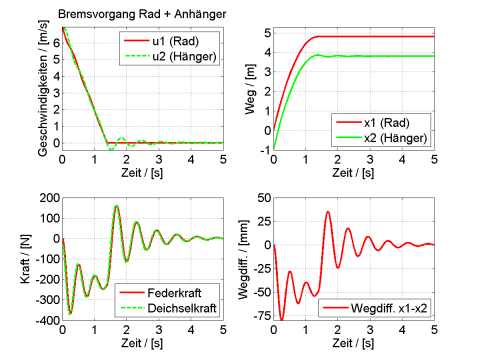
Die Verläufe von Weg und Geschwindigkeiten in Bild 9 und 10 sind insgesamt plausibel. Die Abbremsung dauert etwa 1,5 s. Der Bremsweg beträgt etwa 4 m. Man erkennt in den Kraftschwingungen sowie in den Teilbildern der Relativbewegung (Bilder rechts unten in Bild 9 und 10) auch deutlich ein Nachschwingen des Hängers, nachdem das Rad bereits zum Stillstand gekommen ist. Das konnte bei den Testfahrten ebenfalls beobachtet werden.
Die vom Überschwingen verursachten Druckkraftmaxima liegen etwa zwischen 300 und 400 N. Das kritische Überschwingen ist bei starker Dämpfung geringer als bei schwacher Dämpfung. Es wird dort aber immer noch eine etwa 50 %ige Kraftüberhöhung gegenüber der statischen Bremskraft beobachtet, während die Überhöhung bei der schwächeren Dämpfung von 100 Ns/m an die 80 % beträgt. Die entsprechende große Wegdifferenz von etwa -70 mm dürfte aber zu groß sein, weil die Kupplungsfeder dadurch extrem verbogen werden müsste. In der Realität sollte das durch die in [Huber 2013] befundene progressive Federwirkung verhindert werden.
In den Bildern 9 und 10 erkennt man auch, dass die Deichselkraft im Wesentlichen aus der Federkraft besteht, da die Dämpfungskraft offensichtlich deutlich kleiner ist, weshalb sich Feder- und Gesamtkraft kaum voneinander unterscheiden.
5. Testergebnisse
5.1 Vortests
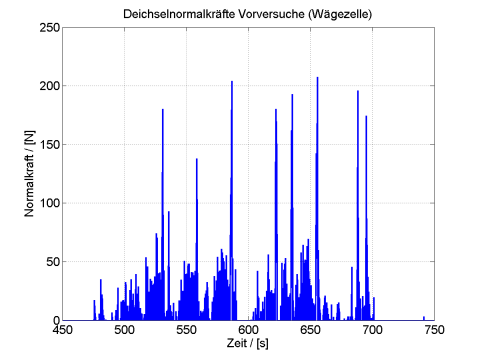
Zunächst wurde eine Reihe von acht aufeinander folgenden Testfahrten gemacht, die in einem gemeinsamen Datensatz abgespeichert wurden. Diese Vortests dienten der Prüfung der prinzipiellen Funktion des Messaufbaus und insbesondere der Klärung der Frage, in welcher Größenordnung die Bremskräfte in der Deichsel liegen. Daher wurde nur das Kraftsignal ausgewertet, das in Bild 11 gezeigt ist. Der dargestellte Messzeitraum umfasst 300 s, worin acht Vollbremsungen an den Kraft-Peaks zu erkennen sind. Die Peaks umfassen jeweils etwa zwei Sekunden Bremszeit, die mit zahlreichen Messpunkten aufgelöst wurden, was hier im Gesamtbild wegen des großen Gesamt-Zeitintervalls jedoch nicht zu erkennen ist.
Die Hauptaussage dieser Abbildung ist, dass in der Deichsel in den Vortests maximale Normalkräfte bis zu einer Höhe von etwa 210 N auftreten. Da die Bremskraft in Fahrtrichtung wirkt, die Deichsel jedoch unter 45 Grad angelenkt ist, kann man die Bremskraft in eine Normal-Komponente in Deichselrohrrichtung (Wägezelle) und in eine Querkraft zerlegen, die ein Biegemoment für die Deichsel bewirkt. Daraus ergibt sich eine maximale Gesamt-Bremskraft von etwa 300 N, was im Bereich der oben dargestellten Rechenergebnisse für die Fälle mit stärkerer Dämpfung liegt.
Neben den hohen Peaks der Bremssignale sieht man in Bild 11 noch zahlreiche niedrigere Kraftspitzen, die von den aus dem Fahrbetrieb überlagerten Deichselschwingungen herrühren. Diese finden sich besser aufgelöst auch in den weiter unten diskutierten Ergebnissen der nächsten Versuchsreihe.
5.2 Zweite Testreihe mit detaillierter Auswertung
In der zweiten Versuchsreihe wurden dann sechs weitere Vollbremsungen und eine schwächere Bremsung unter ansonsten gleichen Bedingungen wie bei den Vortests durchgeführt. Das Rad-Hänger-Gespann wurde dabei jeweils über eine Strecke von etwa 80 m auf etwa 7 m/s beschleunigt und danach durch eine starke Bremsung zum Stehen gebracht. Dabei wurde möglichst versucht, ein seitliches Ausbrechen des Hängers zu vermeiden.
Bild 12 bis 15 zeigen die Versuchsergebnisse jeweils für die Fahrgeschwindigkeit und die Beschleunigung sowie für die Kraftsignale insgesamt und während der Bremsphase. Die Beschleunigungskurven wurden dabei durch Differentiation der Hallgeber-Signale gewonnen. Die Geschwindigkeit ergab sich aus dem Quotienten des Radumfangs durch die Zeitdifferenz zwischen zwei Anstiegsflanken des rechteckförmigen Hall-Signals, das durch zwei gegenüberliegende Magnete mittels eines bipolaren Sensors abgenommen wurde. Eine feinere Auflösung könnte durch Verwendung weiterer am Umfang gleichverteilter Magnete erreicht werden.
Bild 12 zeigt die Geschwindigkeitsverläufe für die zweite Versuchsreihe. Man erkennt, dass jeweils etwa 7…7,5 m/s entsprechend 25…27 km/h als Höchstgeschwindigkeit erreicht werden, bevor dann die Bremsung einsetzt. Die Geschwindigkeitswerte fallen danach stark ab, gehen jedoch nicht ganz auf Null zurück, was von der doch recht groben Diskretisierungs-Schrittweite des Hallgebers herrührt.
Bild 13 zeigt die aus den Hall-Signalen ermittelten Beschleunigungen. Die dargestellten Kurven wurden aus den Roh-Signalen durch einen einfachen Glättungsalgorithmus (5-Punkt-Mittelwert-verfahren) gewonnen, um die bei numerischer Differentiation auftretenden Fluktuationen zu reduzieren. Hier erkennt man zunächst die Beschleunigungsphase mit positiven Werten zwischen 0,5…1 m/s2 und dann die Abbremsphase, wo negative Beschleunigungen zwischen -4,5…-5,5 m/s2 erreicht werden. Das entspricht den typischerweise bei einer guten Fahrradbremse zu erwartenden Werten von über 4 m/s2.
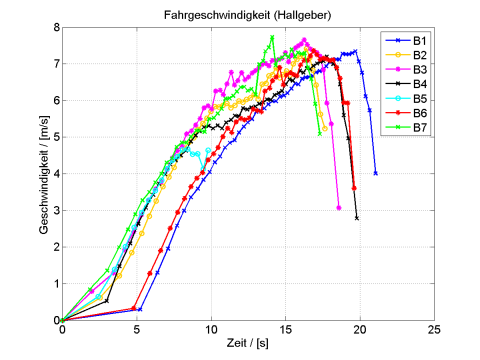
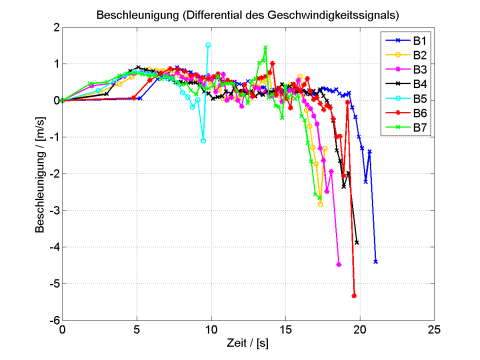
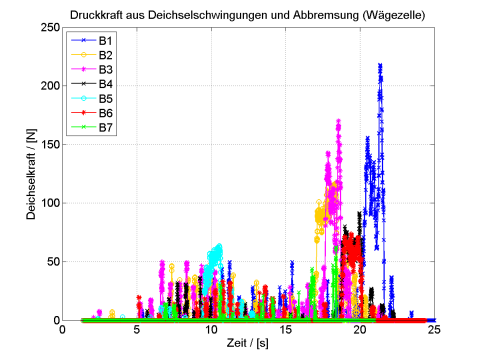
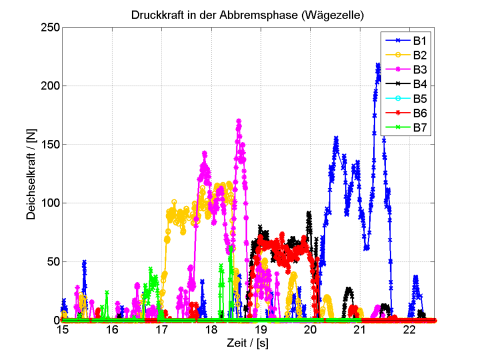
Bild 14 zeigt die Kraftsignale aller sieben Versuche über die gesamte Versuchsdauer. Man kann deutlich die Deichselschwingungen mit niedriger Amplitude von den viel stärkeren Signalen aus der Abbremsphase unterscheiden. Da der Messverstärker nur Druckkräfte verarbeiten konnte, sind nur die Drucksignale sichtbar.
Der besseren Auflösung wegen sind vor allem die interessanten Abbremsphasen zwischen 15 und 22,5 s in Bild 15 noch einmal separat und vergrößert dargestellt. Die Abbremsphasen dauern jeweils zwischen 1,5…2 s und man erkennt in dieser Abbildung auch in den Kraftsignalen überlagerte Schwingungen, die den permanent vorhandenen Deichselschwingungen zugeordnet werden können und die das Kraftsignal gegenüber dem Wert der einfachen Handabschätzung überhöhen, wie es auch vom Zweikörper-Modell prognostiziert wird. Weiter sieht man in Bild 15 z.B. im Fall des Tests B4 (schwarze Kurve) deutlich das Nachschwingen des Hängers nach Ende der Bremsung an den drei danach noch auftretenden Peaks mit abnehmender Amplitude (rechts im Bild), woraus die Dämpfungskonstante berechnet werden kann.
Vor der weiteren Diskussion der Kraftverläufe muss man nun wissen, dass die Deichsel bei Versuch B7 nach insgesamt nur 14 starken Bremsungen partiell gebrochen ist bzw. durch Einknicken in der ersten Biegung unter massiver plastischer Verformung katastrophal versagt hat. Der Beginn der Plastifizierung hat vermutlich bereits nach Test B3 eingesetzt, da in den Tests B4 und B6 (Niederlastfall B5 ist nicht relevant und nur in Bild 14 sichtbar) trotz hoher negativer Beschleunigungen (Höchstwert bei Test B6) nur noch vergleichsweise niedrige Deichselkräfte erreicht werden. In Test B7, in dem die Deichsel endgültig versagte, ist dann überhaupt kein nennenswerter Deichselkraftanstieg beim Bremsen mehr erkennbar. Das weist darauf hin, dass die Deichsel zu diesem Zeitpunkt bereits durch die vorhergegangenen Versuche vorgeschädigt, d.h. eventuell durch plastische Verformung über den Originalkrümmungswinkel gestaucht war, was jedoch nicht unmittelbar augenfällig war. Allerdings wurden auch keine Sichtprüfungen zwischen den Tests durchgeführt, da ein derart frühes Versagen nicht erwartet wurde.
6. Erklärungsversuch für das Deichselversagen
6.1 Phänomenologie
Die Bild 16 bis 17 zeigen die Deichselverformung nach dem Versagen sowie Details der Bruchstelle. Nach den im folgenden gezeigten Spannungsanalysen dürfte der Bruch durch Plastifizierung auf der inneren Druckseite der ersten Deichselkrümmung eingeleitet worden sein. Das dürfte dann zum Einknicken in der Ebene der Deichselschenkel mit seitlicher Ausbeulung und Einrissen an den dort unter 90 Grad entstandenen starken Knicken geführt haben. Weiter findet sich dann noch ein Einriss an der ebenfalls stark gefalteten Innenseite (Druckseite) der ersten Biegung.
6.2 Begleitende Berechnungen
Nachdem die auftretenden Kräfte nun über Messung und Rechnung in etwa bestimmt wurden und insgesamt plausibel erscheinen, kann man an die Ermittlung der Spannung gehen, um der Versagensursache auf die Spur zu kommen.
Der erste Schritt besteht darin, die Biegespannung im kritischen Querschnitt (erste Deichselbiegung) zunächst grob abzuschätzen. Dazu wird das Biegemoment ausgerechnet, das die Querkraft von 210 N (wegen der 45-Grad-Zerlegung gleich der gemessenen Normalkraft) nach etwa 0,5 m an der Stelle der ersten Biegung bewirkt. Über das Widerstandsmoment der Rohres von W = 770 mm3 wird die maximale Biegespannung ermittelt. Daraus ergibt sich dann ein Biegemoment MB = 110 Nm und eine maximale Biegespannung σB = MB/W von 136 MPa [Winkler et al. 1985a], die schon recht nahe bei der Streckgrenze von AlMgSi0,5 von etwa 150…160 MPa liegt [Hoepke 2002].


6.2.1 1D-Rechnung
Im nächsten Schritt wird die Deichselkrümmung berücksichtigt. Dabei wird näherungsweise die Verteilung von Querkraft FQ, Normalkraft FN und Biegemoment MB entlang der Deichsel unter Verwendung der aus den Versuchsergebnissen erhaltenen Belastungsdaten bestimmt. Dazu werden die Differentialgleichungen für FQ, FN und MB entlang der gekrümmten Deichsel integriert (siehe [Dankert et al. 2006a] ).
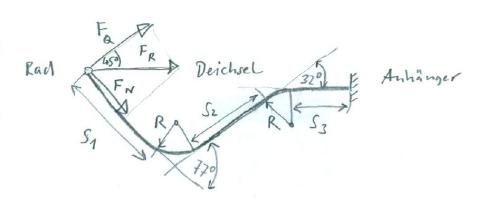
Hierbei bedeutet s die Ortskoordinate entlang der Deichsel und R den Krümmungsradius in den beiden Biegungen. Bild 18 zeigt eine Skizze der Deichsel, in der die Bezeichnungen für die charakteristischen Abmessungen und Winkel angegeben sind. Der Krümmungsradius an den beiden Biegungen beträgt jeweils R = 0,04 m, die geraden Rohrstücke dazwischen haben die Längen S1 = 0,47 m; S2 = 0,33 m und S3 = 0,2 m.
Aus der Momentenverteilung ergibt sich das größte Biegemoment für den Bremslastfall im Bereich der ersten Biegung (kritischer Querschnitt). Dafür wurde die Spannungsverteilung unter Berücksichtigung der Deichselkrümmung näherungsweise nach Dankert [Dankert et al. 2006b] berechnet
Das in Gl. 15 verwendete Formfaktorintegral K wurde für den vorliegenden Rohrquerschnitt in drei Teile zerlegt und dann numerisch integriert. A bezeichnet in Gl. 15 den Rohrquerschnitt und dA ein Querschnittsflächenelement. Mit y ist die lokale Koordinatenachse von der Rohrmitte zum Außenradius bezeichnet.
In den Berechnungen wurde die veränderte Deichselgeometrie (Verlängerung um die Länge der Wägezelle plus Aufnehmer) sowie die maximal in den Versuchen aufgetretene FN = 220 N verwendet. Weiter wurde von einem idealen kreisringförmigen Querschnitt ausgegangen.
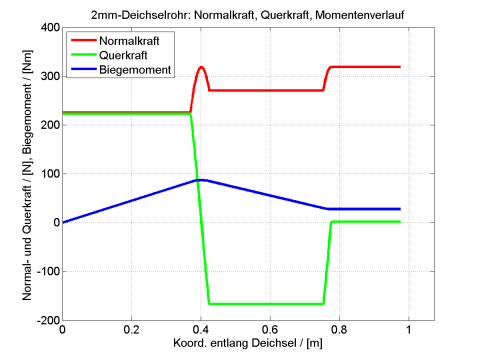
Bild 19 zeigt die Verläufe von Normalkraft, Querkraft und Biegemoment entlang der Deichsel für diesen Lastfall. Man erkennt deutlich die Variationen der Normalkraft in den gekrümmten Regionen und den Vorzeichenwechsel der Querkraft. Außerdem lässt sich ein maximales MB ≈ 110 Nm im Bereich der ersten Biegung ablesen.
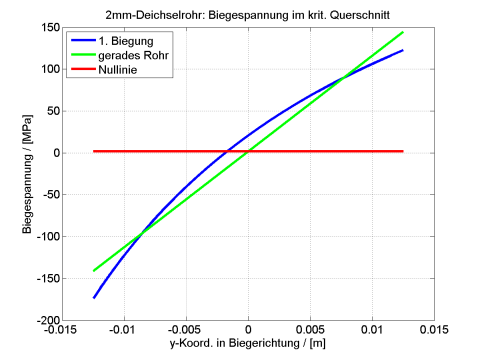
Weiter ist in Bild 20 der Spannungsverlauf im kritischen Querschnitt in der Knickebene gezeigt. Man erkennt deutlich die Spannungsüberhöhung auf der Druckseite bei Berücksichtigung der Krümmung (blaue Kurve) gegenüber der linearen Standardspannungsverteilung (grüne Kurve) beim glatten Rohr. Der Normalspannungsanteil ist mit etwa 2 MPa sehr gering, weshalb vor allem die Biegebelastung kritisch ist. Als maximale Biegespannung in der Druckzone wird ein Wert von etwa 175 MPa erreicht, der bereits über der Streckgrenze für AlMGSi05 von 150…160 MPa liegt [Hoepke 2002] und auf eine mögliche Plastifizierung am Rohrrand hinweist.
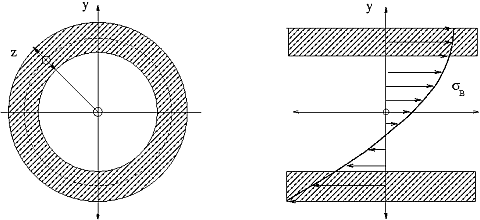
Zur besseren Orientierung über die Lage der Spannungsverteilung und die verwendeten Hilfskoordinaten sind in Bild 21 noch zwei Skizzen angegeben. Links ist die Querschnittskoordinate y gezeigt sowie die Wanddickenkoordinate z, die von der Rohrwandmitte aus gezählt wird und in der im folgenden behandelten zweiachsigen Spannungsbetrachtung auftritt. Weiter ist rechts noch die prinzipielle Lage der Spannungsverteilung nach Gleichung 15 angegeben.
In der Literatur findet man noch weitere analytische Berechnungsformeln für das gekrümmte Rohr unter Biegebeanspruchung. Im Unterschied zu Dankert wird in diesen Beziehungen berücksichtigt, dass sich das gekrümmte Rohr bei der Biegebelastung auch noch elliptisch verformt, wodurch eine zusätzliche Umfangsbiegespannung hervorgerufen wird und somit ein zweiachsiger Spannungszustand entsteht. Unter Berücksichtigung der elliptischen Verformung (im elastischen Bereich) gibt Klapp [Klapp 1970] für die Spannungsverteilung die Beziehung
an. Darin bezeichnet I das Flächenträgheitsmoment des Rohrquerschnitts, Rm den mittleren Rohrradius, RB den Biegeradius und sw die Rohrwandstärke. Schwaigerer [Schwaigerer et al. 1997] gibt ebenfalls Formeln für die Längsbiegespannung im gekrümmten Rohr an, die mit der Koordinate z noch zusätzlich den Spannungsverlauf über die Wandstärke erfasst (gemessen vom mittleren Rohrradius, sodass z = +sw / 2 die Rohraußenseite und z = -sw / 2 die Rohrinnenseite bedeutet, während die Koordinate y den Abstand von der neutralen Faser der Biegung misst. Die Beziehungen von Schwaigerer für Längs- und Umfangsbiegespannung lauten
sowie
mit der Querkontraktionszahl ν = 0,33 und dem Außenradius Ra der Rohres.
Bild 22 zeigt die Auswertung dieser Formeln für den Fall der maximal in den Versuchen erreichten Bremsquerkraft von 220 N bzw. das zugehörige maximale Biegemoment von 110 Nm im kritischen Querschnitt an der Position z = 0 mm, d.h. am Ort des mittleren Rohrradius.
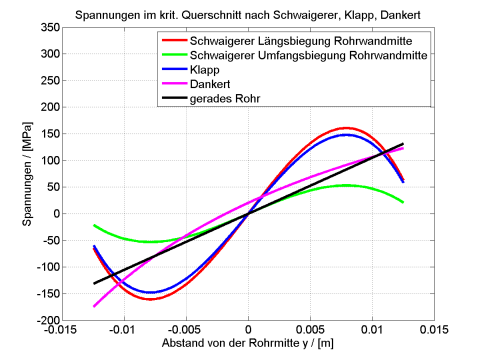
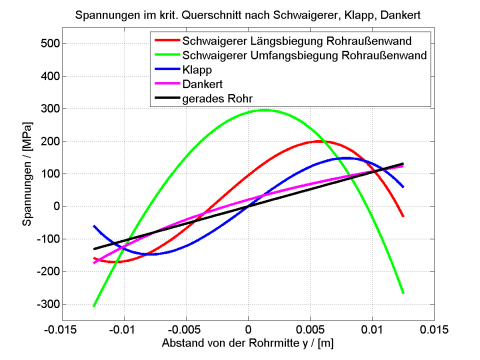
Bild 22: in der Rohrwandmitte
Bild 23: am Rohraußenrand
Man erkennt, dass die Beziehungen von Schwaigerer und Klapp für die Längsbiegung recht ähnlich sind. Sie zeigen sowohl auf der Innen- als auch auf der Außenseite des Rohres ebenfalls eine Spannungsüberhöhung gegenüber dem geraden Rohr, allerdings keine so starke betragsmäßige Erhöhung auf der Druckseite, wie es bei Dankert der Fall ist. Auch hier wird die Streckgrenze erreicht. Die zusätzlich berücksichtigte Umfangsbiegespannung ist in der Rohrwandmitte deutlich kleiner als die Längsbiegespannung. Weiter sind die Spannungsmaxima etwas zur neutralen Faser hin nach »innen« verschoben, was nach Klapp [Klapp 1970] eine Folge der zusätzlichen elliptischen Deformation ist.
Bild 23 zeigt die Spannungsverteilung desselben Lastfalls, wobei nun die Formeln von Schwaigerer an der Rohraußenseite (z = +sw / 2) ausgewertet wurden. Das liefert für den Außenrand des Rohres eine weitere deutliche Spannungserhöhungen für die Längsbiegespannung. Weiter zeigt sich nun die Umfangsbiegespannung als zusätzliche kritische Größe. Die Streckgrenze wird in der zweiachsigen Analyse sowohl in der Ebene der neutralen Faser der Längsbiegung als auch am Rohrrand an der Innen- und Außenbiegung deutlich überschritten.
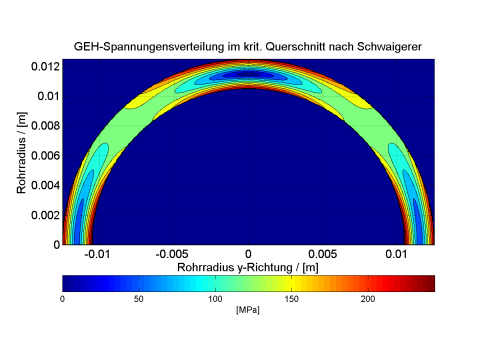
Da die Formeln von Schwaigerer einen zweiachsigen Spannungszustand beschreiben, sind hierfür zum Vergleich mit den unten dargestellten FEM-Rechenergebnissen in Bild 24 noch die Vergleichsspannungen nach Gestaltänderungshypothese (GEH) [Winkler et al. 1985b] als Konturplot im kritischen Rohrquerschnitt dargestellt, wobei etwaige Schubspannungen als klein gegenüber den Biegespannungen angesehen und vernachlässigt werden. Man erkennt in Bild 24 deutlich die Spannungsmaxima an der Innen- und Außenbiegung links und rechts im Bild sowie in der neutralen Faser der Deichselkrümmung (Bildmitte), die unmittelbar an der Rohrwand auftreten. In der Mitte der Rohrwand sind diese Maxima dagegen nicht mehr zu sehen, d.h. die sehr hohen Randspannungen klingen zur Wandmitte hin wieder ab, sodass vor allem am Rand plastisches Verhalten auftreten dürfte.
Zusammenfassend kann man aus den dargestellten Rechenergebnissen folgern, dass alle Rechenmodelle lokale Spannungsüberhöhungen zeigen, die deutlich über der Streckgrenze liegen. Das detaillierte zweiachsige Modell von Schwaigerer zeigt zusätzlich kritische Umfangsbiegespannungen in der neutralen Faser der Längsbiegung sowie gegenüber der einachsigen Betrachtung erhöhte Längsbiegespannungen. Das bestätigt und verstärkt somit die Indizien für die Gefahr des Bauteilversagens.
6.2.2 FEM-Berechnungen
Zur weiteren Absicherung der Ergebnisse wurden noch Rechnungen mit dem an der Universität Bayreuth entwickelten freien FEM-Programm Z88 Aurora [Rieg et al. 2012] durchgeführt. Dazu wurde eine STL-Datei für die Deichsel mit den oben angegebenen Abmessungen und Biegewinkeln erstellt. Allerdings wurde die Länge S1 (von der Kupplung bis zur ersten Biegung) von 0,47 m auf 0,37 m verkürzt, was eher der tatsächlichen Deichsellänge ohne den zusätzlich eingebauten Kraftaufnehmer entspricht.
Aus der STL-Datei wurde mit dem Netzgenerator TETGEN ein Netz mit etwa 30.000 Knoten und etwa 100.000 Elementen erzeugt. Für die Berechnungen wurde die Deichsel am hängerseitigen Ende als fest eingespannt betrachtet (keine Verschiebungen), während am radseitigen Ende der Deichsel die Bremskraft zerlegt in Normal- und Querkraft entsprechend der 45-Grad-Anlenkung aufgebracht wurde. Es wurden verschiedene Lastfälle mit Normal- und Querkräften von 155…250 N berechnet, wie sie auch in den Messungen in etwa aufgetreten sind. Zur Lösung wurde der in Z88 eingebaute Konjugierte-Gradienten-Solver mit Vorkonditionierung SICCG verwendet.
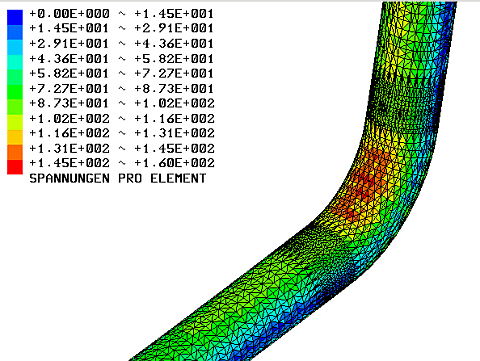
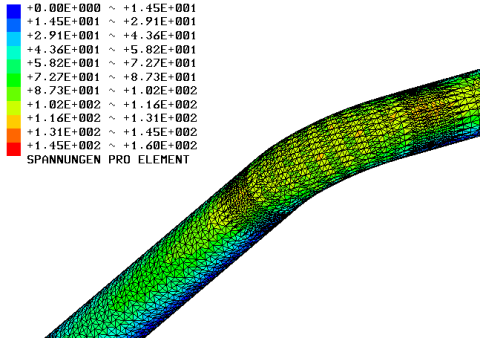
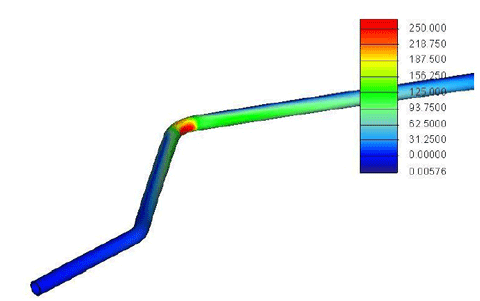
Die Ergebnisse der FEM-Rechnungen mit Z88 Aurora sind in Bild 25 und 26 für den Fall einer Normalkraft von 250 N gezeigt. Die dargestellten Elementspannungen werden in Z88 Aurora mittels der GEH aus den benachbarten Knotenspannungen ermittelt. Man sieht aus den Bild 25 und 26, dass die maximalen Spannungen in Übereinstimmung mit der Theorie des gekrümmten Trägers nach Dankert auf der Druckseite entstehen und im dargestellten Fall von FN = 250 N die Streckgrenze von etwa 160 MPa erreicht wird. Die zusätzlichen Spannungen aus der elliptischen Deformation werden in dieser einfachen FEM-Rechnung nicht dargestellt, was an der ungenügenden Auflösung der Rohrwand durch nur eine Schicht von Tetraeder-Elementen liegt.
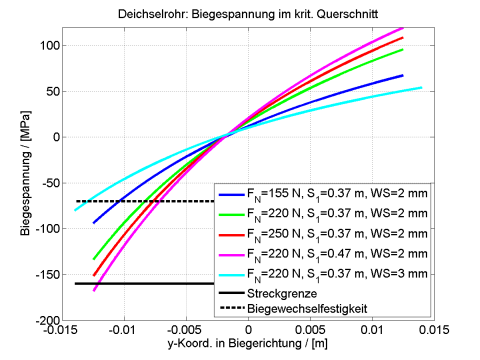
Wegen der Verkürzung der Deichsel wird die Streckgrenze hier im Unterschied zu Bild 19–21 erst bei einer etwas höheren Normalkraft von 250 N überschritten, was einer Bremskraft von etwa 350 N entspricht. Zum Vergleich wurde deshalb auch mit dem 1D-Modell nochmals die Spannungsverteilung im kritischen Querschnitt für die drei Lastfälle mit der um 10 cm kürzeren Deichsel berechnet, was in Bild 27 dargestellt ist. Man erkennt daraus, dass die quantitative Übereinstimmung der maximalen Druckspannungen aus der obigen FEM-Rechnung mit einschichtigen Tetraeder-Elementen und dem 1D-Modell recht gut ist (ca. 160 MPa in der FEM-Rechnung von Bild 25 und 150 MPa in der korrespondierenden rot markierten Kurve in Bild 27). Weiter sind zum Vergleich noch der Fall der um den Messaufnehmer verlängerten Deichsel sowie eine Vergleichsrechnung mit auf 3 mm erhöhter Wandstärke eingetragen. Man erkennt, dass die Fälle mit 2 mm Wandstärke bei Normalkräften über 200 N sehr nahe an oder schon über der Streckgrenze von 160 MPa liegen, während nur der Fall mit erhöhter Wandstärke von 3 mm eine akzeptable Sicherheit liefert. Die für dynamische Belastung maßgebliche Biegewechselfestigkeit von 70 MPa [Senkel 1998] wird in allen Fällen überschritten.
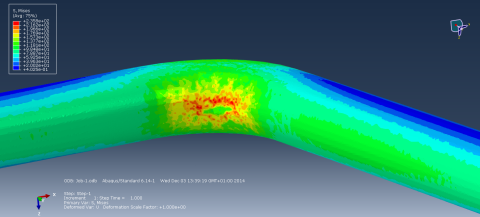
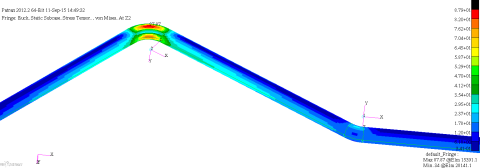
Eine Vergleichsrechnung, die mit einem feineren Netz (ca. 3 Millionen Elemente) und dem FEM-Programm Abaqus an der Universität Bayreuth durchgeführt wurde, bestätigt diesen Befund [Frisch] . Hier treten ebenfalls deutlich über der Streckgrenze liegende Spannungen an der Innenbiegung auf, (s. Bild 28), die maximal 235 MPa erreichen. Die im Vergleich zu Z88 höheren Werte können damit erklärt werden, dass hier die Rohrwand radial mit mehreren Schichten aufgelöst wird, während in Z88 nur eine Schicht von Tetraeder-Elementen verwendet wurde, was eher zu den in Bild 22 dargestellten mittleren Werten passt. Allerdings werden in der Abaqus-Rechnung wie auch in der Z88-Rechnung die recht hohen Spannungen in der Ebene der neutralen Faser der Biegung, die nach den genaueren analytischen Formeln von Schwaigerer auftreten sollten, nicht wiedergegeben. Eine Erhöhung auf 120 MPa sieht man aber dennoch. Wie oben schon erwähnt, klingen die Randspannungen nach Schwaigerer zur Rohrwandmitte hin rasch ab, was auch auf dem feinen Netz bei zu geringer radialer Auflösung zu niedrigeren gemittelten Spannungen führen dürfte, als der exakte Randwert in der analytischen Lösung angibt.
Zwei weitere Vergleichsrechnungen zur vorliegenden Problemstellung wurden von der Höheren Technischen Bundeslehr- und Versuchsanstalt Salzburg [Landertshamer] sowie von O. Schultz [Schultz] durchgeführt. Erstere verwendet PTC Creo Parametric (Elementierung: Tetraeder), zweitere MSC NASTRAN (Elementierung: CQUAD4), die der Problemstellung besser angepasst sind als die z.B. in Z88 verwendeten Tetraeder-Elemente.
Auch diese Rechnungen zeigen deutlich die Spannungsüberhöhung an der Innenseite der Deichselbiegung. Weiter kann man hier nun auch die zusätzliche Spannungserhöhung aus der elastischen elliptischen Verformung erkennen, die in der Ebene der neutralen Faser der Biegung auftritt (s. Bild 29 und 30). Für einen direkten Vergleich sind die Spannungen in Bild 30 mit einem Faktor 3 zu multiplizieren, da hier mit einer Bremskraft von 100 N gerechnet wurde.
Da eine wichtige Ursache für das Überschreiten der Streckgrenze die Spannungsüberhöhung durch die bauartbedingte Krümmung der Deichsel sein dürfte, wurde noch der Effekt des Krümmungsradius auf die Spannungsverteilung im kritischen Querschnitt untersucht. Dazu wurden Rechnungen bei fixem Winkel von 77 Grad in der ersten Biegung, aber mit variiertem Krümmungsradius mit der 1D-Theorie des gekrümmten Trägers nach Dankert durchgeführt. Dabei zeigte sich, dass eine Erhöhung des Krümmungsradius in zweierlei Weise günstig ist: Zum einen wird die Spannungsüberhöhung auf der Druckseite reduziert, zum andern wird auch noch der maximale Hebelarm der Bremskraft reduziert, da der Krümmungsscheitel nach innen hin zur Fahrzeuglängsachse rückt.
Bild 31 zeigt die Spannungsverteilung bei einer Querkraft von etwa 220 N, die dem Testlastfall entspricht, für von 20 mm auf 300 mm anwachsende Krümmungsradien. Bei den zuvor gezeigten Ergebnissen war der Krümmungsradius mit etwa 40 mm ungefähr gleich dem Wert der Testdeichsel gewählt worden (Referenzfall). Die Länge des ersten Deichselteilstücks S1 beträgt im Referenzfall wiederum 0,37 m, hat also den um die Messaufnehmerlänge von 0,1 m reduzierten Wert. Für die modifizierten Krümmungsradien wurden die geraden Deichsellängenstücke entsprechend abgeändert, sodass jeweils Anfangs- und Endpunkt sowie die sich aus den Tangenten ergebenden »Knickpunkte« erhalten blieben.
Man erkennt in Bild 31 erwartungsgemäß, dass ein gegenüber dem Referenzwert von 0,04 m reduzierter Krümmungsradius weitere Spannungserhöhung bewirkt, während mit zunehmenden Radien sowohl die Spannungsüberhöhung als auch die Maximalspannung stark abnehmen. Demnach bietet sich auch ein erhöhter Krümmungsradius als geeignete konstruktive Maßnahme zur Verbesserung der Deichselsicherheit an. Allerdings sind der Erhöhung des Krümmungsradius durch die Manövrierfähigkeit des Gespanns Grenzen gesetzt (Anstoßen des Hinterrades an der Deichsel beim Rangieren).
Zusammenfassend ergibt sich als Ergebnis der dargestellten Berechnungen, dass das maximale Biegemoment beim Bremsen an der Stelle der ersten Deichselbiegung auftritt. Dieses Moment verursacht den Hauptanteil der aus Normal- und Biegespannungen zusammengesetzten Gesamtspannung im kritischen Querschnitt. Durch die Krümmung wird die Biegespannung auf der Druckseite gegenüber den Verhältnissen beim geraden Rohr am Innenrand deutlich verstärkt. Auf der Zugseite entstehen ebenfalls starke Spannungserhöhungen. Auch in der neutralen Faser der Biegung finden sich große Spannungserhöhungen, die von der mit der Längsbiegung einhergehenden elliptischen Deformation verursacht werden.

Die Unterschiede in den Details der einzelnen Berechnungen können jeweils auf die unterschiedlichen Modellvereinfachungen (einachsig/zweiachsig bzw. Netzeffekte bei FEM) zurückgeführt werden, ergeben aber insgesamt ein konsistentes Bild. Alle Rechenmodelle zeigen letztendlich als übereinstimmendes Hauptergebnis, dass sich bei der aus Versuchen und Rechnungen ermittelten Bremskraft an der Innenseite der Deichselkrümmung kritische Spannungen ergeben, die in der Nähe der Streckgrenze des verwendeten Werkstoffs liegen oder darüber hinausgehen.
6.3 Versagensmechanismus
Zur Erklärung des beobachteten Deichselbruchs wird folgender Versagensmechanismus vorgeschlagen:
Verursacht durch das Überschwingen der Deichselkraft über die Gleichgewichtslage im Zusammenwirken mit der Kupplungsfeder ergeben sich an der Stelle der ersten Deichselkrümmung an der Innen- und Aussenseite des Rohres in Biegerichtung starke Spannungsanstiege, die zu lokaler Plastifizierung führen können. Dadurch gibt die Deichsel in Richtung der Bremskraftbelastung nach, der Biegewinkel vergrößert sich etwas, was wiederum die Krümmung erhöht und bei der nächsten Belastung wegen verstärkter Spannungsüberhöhung noch günstigere Bedingungen für die Plastifizierung schafft. Dies kann dann durch mehrmalige Bremsvorgänge bei immer niedrigeren Kraftamplituden geschehen, was schließlich zum Versagen der Deichsel führt. Die stückweise erfolgenden Erhöhungen des Krümmungsradius sind dabei vermutlich recht klein und somit auch bei Sichtkontrolle nicht leicht wahrnehmbar. Daher besteht die Gefahr eines plötzlichen und unerwarteten Versagens.
Da die verwendete Deichsel bereits im unbelasteten Zustand eine elliptische Verformung des Querschnitts zeigte, die durch einen nicht optimalen Biegevorgang bei der Herstellung verursacht war, wurde die damit verbundene Beeinträchtigung der Deichselstabilität abgeschätzt. Ein Vergleich der Widerstandsmomente gegen Biegung zwischen Kreisringquerschnitt und elliptisch verformtem Querschnitt ergab W = 770 mm3 für den Idealfall und W = 607 mm3 für den elliptisch verformten Fall (bei einem Halbachsenverhältnis von 13,75/10 mm) [Klepp et al. 1987] . Dadurch ergibt sich eine um 26 % höhere Biegespannung, die allerdings in der Rechnung nicht berücksichtigt wurde, da sich, wie gezeigt, bereits mit dem sichereren Kreisringquerschritt plastisches Verhalten ergibt. Die Rechenergebnisse würden also für elliptisch vorverformten Querschnitt noch deutlicher auf Plastifizierung hinweisen.
Zum anderen wurden die Testfahrten nur mit 75 % der Nennlast durchgeführt, weshalb sich bei Vollast die Gesamtmasse um 22,5 % erhöht und man eine entsprechende Vergrößerung der Bremskraft und damit auch der kritischen Biegespannung erwarten kann. Zudem sind bei modernen Fahrrädern Bremsverzögerungen von über 5 m/s2 möglich, was zu einer weiteren Erhöhung der Bremskraft und entsprechend höheren Deichselbelastungen führen würde. Zur Entschärfung der Situation trägt bei, dass das Biegemoment bei der um den Messaufnehmer verkürzter Deichsel tatsächlich geringer ist und dass die Plastifizierung der Randzone zunächst noch kein Versagen, sondern sogar eine Traglasterhöhung bewirken kann [Dimitrov 1971] , was für gerade Träger auch als plastische Reserve bezeichnet wird. Nach dem oben angegebenen Versagensmechanismus sollte die wiederholte Belastung aber eine schrittweise Erhöhung des Krümmungswinkels bewirken, die auch die Plastifizierung bis zum Versagen fortschreiten lässt.
Zusammenfassend ergibt sich daher aus den durchgeführten Untersuchungen, dass die verwendete Auslegung der Deichsel mit D = 25 mm bei 2 mm Wandstärke und dem Werkstoff AlMgSi0,5 nicht als betriebssicher angesehen werden kann. Bereits bei nur 75 %iger Beladung wird schon der Bereich der Streckgrenze erreicht, sodass keinerlei Sicherheitsbeiwert vorhanden ist. Dementsprechend wird zuvor schon die viel niedrigere zulässige Spannung von etwa 70 MPa für die Biegewechselfestigkeit, die eigentlich für die Auslegung heranzuziehen wäre, deutlich überschritten.
7. Verbesserungsvorschläge
Als Abhilfemaßnahmen bieten sich die folgenden Dinge an:
- Einziehen eines Drahtseils in die Deichsel. Das kann zwar das Auftreten eines Schadens nicht verhindern, vermeidet aber zumindest ein unkontrolliertes komplettes Abreißen der Deichsel mit unkontrollierter Entfernung des Hängers vom Rad.
- Austausch der Deichsel durch eine Variante mit erhöhter Wandstärke oder andere Werkstoffauswahl mit höherer Festigkeit (z.B. AlMgSi1 (EN AW- 6082), Streckgrenze etwa bei 240 MPa).
- Reduktion des Überschwingens durch anderes Kupplungssystem oder Einbau geeigneter Dämpfungselemente.
- Reduktion der Krümmungsradien der Biegungen, soweit das im Hinblick auf die Manövrierfähigkeit beim Rangieren möglich ist.
- Einbau einer Querstrebe in die erste Krümmung. Dadurch wird die Krümmung ausgesteift und ein Abknicken zuverlässig verhindert.
Vor allem die letzte Maßnahme kann mit wenig Aufwand durchgeführt werden, um die Sicherheit einer bestehenden Deichsel ohne Neuanfertigung und Tausch zu verbessern (s. Bild 32 und 33). Allerdings sollte die Querstrebe vorzugsweise geklemmt oder mit Schellen befestigt und nicht geschraubt werden, sodass keine weiteren Spannungsspitzen durch Kerbwirkung im Bereich der ansonsten erforderlichen Bohrungen entstehen.
Generell kann man sagen, dass man beim Selbstbau von Radanhängerdeichseln eine ausreichend hohe Streckgrenze des Materials und großzügige Dimensionierung wählen muss, sodass die Biegewechselfestigkeit des Werkstoffs nicht überschritten wird und Plastifizierungen an den Knickstellen der Deichsel sicher vermieden werden. Die Finite-Elemente-Analyse, die heute auch für fachlich interessierte und engagierte Laien mittels freier Programme, wie z.B. Z88 Aurora, nutzbar ist, kann für die Auslegung mit Vorteil eingesetzt werden. Es ist aber ratsam, auch Handabschätzungen und analytische Methoden zur Kontrolle anzuwenden.


Danksagung
Die Autoren möchten den folgenden Personen herzlich für ihre Unterstützung bei der Abfassung dieses Beitrags danken:
- Prof. Dr. J. Dankert, Jesteburg, für die kritische Durchsicht und hilfreiche Kommentare.
- Prof. Dr. T. Antretter, Institut für Mechanik, Montanuniversität Leoben, für die Überprüfung der rechnerischen Abschätzung der Belastungen bei den Bremstests.
- Dr. M. Frisch, Lehrstuhl für Konstruktionslehre und CAD, Universität Bayreuth, für die Unterstützung bei Z88 Aurora und Nachrechnung mit dem FEM-Programm Abaqus.
- Dr. L. Stumpfrock, Staatliche Materialprüfungsanstalt, Stuttgart, für die Durchführung eines statischen Festigkeitsnachweises mit Nennspannungen in Anlehnung an die FKM-Richtlinie (mit leider negativem Ausgang, Auslastungsgrade für Zustände T4 und T6 beide über 1).
- Dr. F. Landertshamer, Höhere technische Bundeslehr- und Versuchsanstalt, Salzburg, für die Begutachtung der Auslegung und Durchführung von weiteren FEM-Rechnungen sowie hilfreiche Vorschlägen für die Verbesserung der Konstruktion.
- DI Olaf Schultz, Hamburg, für zusätzliche Nachrechnungen mit NASTRAN unter Verwendung von CQUAD4-Elementen sowie für zahlreiche nützliche Hinweise zur inhaltlichen und formalen Verbesserung der durchgeführten Sicherheitsanalyse.
Der Ordnung halber soll noch darauf hingewiesen werden, dass die hier näher untersuchte Deichselauslegung von anderen Fachleuten scheinbar doch als akzeptabel angesehen wird. So hat Prof. M. Bader vom Institut für Maschinenelemente und Entwicklungsmethodik der TU Graz, der zwei Bachelor-Arbeiten zum Radanhängerbau für das eingangs genannte Sozialprojekt in Graz betreut hat [Huber 2013] [Striedner 2013] , auch nach Vorlage der obigen Z88 FEM-Rechnungen und der Ergebnisse der Belastungstests die ursprüngliche Werkstoffwahl und Dimensionierung der Deichsel nochmals bestätigt, wonach die »konstruktive Auslegung in Ordnung« sei und »aufgrund rechnerischer Auslegung kein Handlungsbedarf« bestehe [Bader 2014] . Die Fachwelt ist sich da also anscheinend nicht ganz einig. Die Autoren raten aber zur bewährten Maxime: »Vorsicht ist die Mutter der Porzellankiste.«
Zu den Autoren
 Eberhard
arbeitet als Ingenieur in der Dieselmotorenentwicklung. Lukas studiert
Verfahrenstechnik an der Montan-Universität Leoben. Beide fahren gern
Rad – mit und ohne Anhänger.
Eberhard
arbeitet als Ingenieur in der Dieselmotorenentwicklung. Lukas studiert
Verfahrenstechnik an der Montan-Universität Leoben. Beide fahren gern
Rad – mit und ohne Anhänger.
Literatur
- Bader 2014
- Prof. Dr. M. Bader, MEEM, TU Graz, persönliche Mitteilung (per E-Mail vom 14.11.2014)
- Dankert et al. 2006a
- J. u. H. Dankert: Technische Mechanik. 4. Auflage. Teubner-Verlag, 2006. S. 304 ff.
- Dankert et al. 2006b
- ebd. S. 309
- Dimitrov 1971
- N. Dimitrov. Festigkeitslehre I. Berlin 1971. S. 160
- Frisch
- Dr. M. Frisch, Uni Bayreuth, persönliche Mitteilung
- Hoepke 2002
- Erich Hoepke (Hg.): Nutzfahrzeugtechnik. 2. Auflage. Vieweg-Verlag, Wiesbaden 2002. S. 193
- Huber 2013
- K. Huber: Versuchs- und simulationsgestützte Beschreibung und Optimierung eines Fahrradanhängers. Bachelorarbeit. TU Graz, 2013
- Klapp 1970
- E. Klapp: Festigkeit im Apparate- und Anlagenbau. Düsseldorf 1970. S. 83 ff.
- Klepp et al. 1987
- H. Klepp, T. Lehmann: Technische Mechanik Bd. 1. Heidelberg 1987. S. 539
- Kurzweil 2009
- P. Kurzweil: Physik-Formelsammlung. 2. Auflage. Vieweg, 2009. S. 17 1 ff
- Landertshamer
- Dr. F. Landertshamer, HTBLuVA Salzburg, persönliche Mitteilung
- Rieg et al. 2012
- F. Rieg et al.: Finite Elemente Analyse für Ingenieure. 4. Auflage. Hanser Verlag, 2012
- Schultz
- Olaf Schultz, Hamburg, persönliche Mitteilung
- Schwaigerer et al. 1997
- S. Schwaigerer, G. Mühlenbeck: Festigkeitsberechnung im Dampfkessel-, Behälter- und Rohrleitungsbau. 5. Auflage. Springer Verlag, 1997. S. 8 5 ff
- Senkel 1998
- Thomas Senkel: Aluminium im Bau von Leichtfahrzeugen. In: Proceedings of the Third European Seminar on Velomobile Design. Roskilde Technical School. August 5th 1998. S. 189-196
- Striedner 2013
- C. Striedner: Konstruktion eines Fahrradanhängers und die Umsetzung und Fertigung im Rahmen eines Sozialprojekts. Bachelorarbeit. TU Graz, 2013
- Winkler et al. 1985a
- J. Winkler, H. Aurich: Technische Mechanik. 3. Auflage. Leipzig 1985. S. 128
- Winkler et al. 1985b
- ebd. S. 208