Ausgabe 0 · Februar 2006
Diesen Artikel als PDF
Federung für Liegeräder
Zuerst erschienen 1992 in Pro Velo 29
Der durch eine gute Federung erreichbare Gewinn an Fahrkomfort und Schonung von Wirbelsäule, Nieren, Rahmen, Reifen, Felgen, Speichen, Naben und Gepäck wird immer noch unterschätzt. Da im Gegensatz zum Normalrad die Beine nicht einen Teil des Gewichts tragen und der Fahrer grobe Stöße nicht mit den Beinen abfangen kann, ist eine Federung noch wichtiger. Andererseits sind beim Normalrad keine großen Federwege möglich.
Bei 10 cm Federweg hinten und vorn muß das Tretlager auch 10 cm höher liegen, damit man beim vollen Durchfedern in der Kurve nicht mit dem Pedal aufsetzt. Bei höherem Tretlager muß aber auch der Sattel höher liegen, und da bekommt man sehr schnell Probleme mit der Sitzhöhe, man erreicht im Stehen nur noch mit der Fußspitze oder gar nicht mehr den Boden. Diese Einschränkungen entfallen beim Liegerad völlig. Allerdings nützt außer Ostrad kein Hersteller die Möglichkeit, ein wirklich komfortabel gefedertes Rad zu bauen.
Ich kann nur jedem raten, vor Diskussionen eine Probefahrt auf schlechter Straße mit einem gut gefedertem Rad zu machen, das komfortabelste Liegerad auf dem Markt ist meines Erachtens das genannte Ostrad.
Die einfachste Möglichkeit ist die Abfederung des Sitzes. Der Drehpunkt sollte mindestens 20 cm vor dem Sitz liegen, der Federweg an der Hinterkante mindestens 10 cm betragen. Nachteilig ist, daß die Lehne beim Federn etwas nach hinten nachgibt. Zur verdrehsteifen Führung des Sitzes sollten neben dem Lager auch die seitlichen Streben benützt werden (auf Polyamidblöcken gleiten lassen).
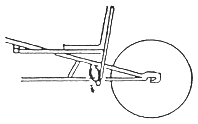
Noch wirksamer ist vor allem beim Langliegerad eine gute Hinterradfederung, an die folgende Anforderungen zu stellen sind:
Sie soll – ausreichend Federweg haben (min. 100 mm) – ausreichend weich sein (Eigenfrequenz beim Wippen durch den Fahrer höchstens 150/min) – nach oben und unten elastische Anschläge haben – die Kette weder an der Schwinge noch am Rahmen voll ein- und ausgefedert, weder im größten noch im kleinsten Gang, weder mit dem oberen noch mit dem unteren Trum anschlagen lassen – beim Treten wenig federn – einstellbar auf verschiedene Gewichte sein – wartungs- und spielfreie Lager haben – das Rad exakt führen (steifer Rahmen, steife Schwinge) – auch auf kleine Unebenheiten leicht ansprechen – sich auch in Schlaglochserien nicht aufschaukeln
Der Bauaufwand steigt allerdings sehr, vor allem wegen der vielen anzufertigenden Kleinteile.
Beispiele für Federungen
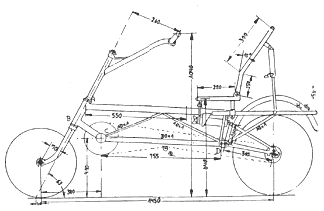
ca. 100 mm Federweg
PU-Block 60 mm × 110 mm lang
auf Druck beansprucht
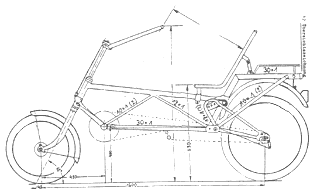
ca. 90 mm Federweg
6 Gummiringe auf Zug
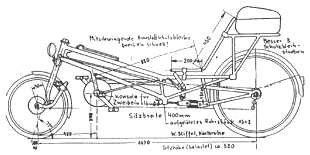
Hinten ca. 130 mm Federweg,
Eigenfrequenz ca. 120/min
geteiltes Schwingenlager,
8 Gummiringe auf Zug
Federelemente für Federungen
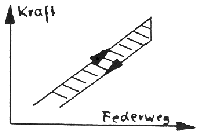
Verwendet werden vor allem Stahlfedern, Gummi- und PU-Blöcke. Für Selberbauer kommen auch auf Zug beanspruchte Gummiringe in Frage. Alles dies wird im Folgenden der Einfachheit halber als Feder bezeichnet. Das wichtigste Kennzeichen einer Feder ist die Federzahl, die angibt, um wieviel Newton die Federkraft beim Einfedern um einen cm ansteigt. In Bild 5 gehört A zu einer weichen, B zu einer harten Feder.
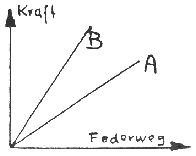
Wenn 2 Federn nebeneinander angeordnet werden (»parallel geschaltet«) addiert sich die Federzahl, Schaltet man die Federn hintereinander, dh. z. B. man hängt 2 Zugfedern hintereinander, halbiert sich die Federzahl, man hat aber bei gleicher Federbeanspruchung den doppelten Federweg.
Da die Feder meist mit einer Übersetzung angreift, das heißt, das Hinterrad legt einen anderen Weg zurück als die Feder, muß alles umgerechnet werden. Rechenbeispiel: eine Schwinge habe das Hebelverhältnis a:b = 200:400 und die Feder eine Federzahl von 500 N/cm. Die auf die Radachse bezogene Federzahl beträgt dann
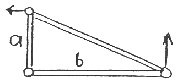
Das Hebelverhältnis geht also quadratisch ein.
Mit Gummiringen kann man sehr leicht durch Verändern der Anzahl die Federzahl variieren. Auf Druck beanspruchte Elemente haben den Vorteil, daß bei Überlastung nichts reißen kann. PU-Schaum hat darüber hinaus den Vorteil, daß er nahezu volumenstabil ist, das heißt sich nicht durch »nach innen wachsen beim Federn« auf dem Führungsbolzen verklemmen kann, außerdem ist seine Federzahl weniger temperaturabhängig als die von Gummi.
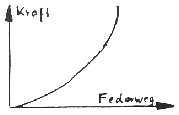
Wünschenswert sind Federn mit einer progressiven Kennlinie, das heißt die Feder wird mit zunehmender Einfederung immer härter (siehe Skizze).
Die Feder ist dann im normalen Arbeitsbereich weich und komfortabel, schlägt aber trotzdem bei höherer Last oder extremen Stößen nicht durch. Bei richtiger Auslegung kann man sich dann unter Umständen die Verstellung sparen. Progressiv sind z. B. alle auf Druck beanspruchten Gummi- oder PU-Blöcke. Eine elegante Lösung sind fertige Federelemente mit Gummischubfedern, z. B. sogenannte Rosta-Elemente, Vierkantrohre mit einen innenliegenden weiteren Vierkant, der beim Verdrehen eingepreßte Gummistränge zusammendrückt. Dieses Federelement ist gleichzeitig eine spiel- und wartungsfreie Lagerung. Ähnlich arbeiten die Elemente von Kronrohr.
Arbeitsvermögen von Federn
Ein wichtiges Kriterium für die Auswahl von Federn ist das Arbeitsvermögen, etwas anschaulicher vielleicht die maximale Stoßenergie, die sie auf Dauer »verkraftet«.
Um welche Beträge handelt es sich? (würde ein Kaufmann sagen). Das Arbeitsvermögen E einer Feder beträgt bei linearer Kennlinie
(E = Arbeitsvermögen, s = maximal erträgliche Längenänderung, P = Kraft, die dabei auftritt)
Der Einfachheit halber stellen wir uns vor, daß eine Feder direkt an der Hinterachse eines Liegerads angreift. Die statische Belastung sei 600 N, dann ist die maximal auftretende Stoßkraft etwa 1500 N. Wenn man dabei einen Federweg von 15 cm (einschließlich Weg bei statischer Belastung) haben will, ist das insgesamt erforderliche Arbeitsvermögen also
Die von mir verwendeten Gummiringe aus Auspuffaufhängungen haben ein
Arbeitsvermögen von etwa 11 Nm, man braucht für eine Hinterradfederung
also
Diese Ringe kann man nun etwa alle parallel, das heißt nebeneinander am Hebelarm 1:2 (Bild 1) oder je 5 hintereinander mit dem Hebelarm 1:1 (Bild 2) anordnen. Wenn man die 10 Ringe am Hebelarm 1:1 anbringt (Bild 3) sind zwar die Ringe nur halb so hoch beansprucht wie bei 1 und 2, die Federung ist aber viel zu hart (Federzahl verdoppelt). Wenn man 5 Ringe am Hebelarm 1:1,4 anordnet, stimmt zwar die Federzahl, die Ringe sind aber viel zu hoch beansprucht.
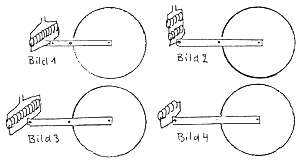
Die zulässige Beanspruchung von Federn ist nicht ganz leicht zu berechnen. Ein Anhalt: Für die Hinterschwinge sollte man das Hebelverhältnis so wählen, daß mindestens 6 Ringe erforderlich sind (z. B. bei meinem Modell »Diogenes« 40:18 und 8 Ringe).
Eigenfrequenz
Ein gutes Maß für den zu erwartenden Fahrkomfort ist die Eigenfrequenz des Fahrzeugs.
(S = Eigenfrequenz, c = Federzahl an der Achse gemessen, m = schwingende Masse)
Ziemlich genau kann die Eigenfrequenz auf folgende Weise gemessen werden: der Fahrer setzt sich in normaler Position auf das Rad, und ein Helfer bringt die Federung durch rhythmisches Drücken zum Federn.
Bei s über 200 wird lediglich die Rahmenbeanspruchung vermindert,
Energieverlust durch Treten
Die meisten Leute gehen davon aus, daß starkes Federn des Hinterrades beim Treten einen direkten Energieverlust bedeutet, weil die beim Anheben des Fahrzeugs geleistete Hubarbeit nicht zurückgewonnen wird. Dahinter steckte für mich folgende Überlegung: Wenn ein Mensch mit senkrecht nach oben gestreckten Beinen auf dem Rücken liegt und auf den Füßen liegt ein schweres Gewicht, dann hat er beim Anziehen der Beine physikalisch gesehen zwar Energie gewonnen (die vorher in dem höher liegenden Gewicht steckte), physiologisch gesehen mußte er sich aber anstrengen, um das Gewicht zu senken.
Wilfried Schmidt (ja, der mit dem SON-Nabendynamo) überraschte mich dann durch die Behauptung, dies sei auf den Fall »Federn beim Treten« nicht anzuwenden. Folgende Überlegungen zeigen meines Erachtens, daß er Recht hat:
Bei meinem »Alfa« mit sehr weicher Federung und Drehpunkt der Schwinge ca. 60 mm unter der Kette führt starkes Treten zu starkem Anheben des Schwerpunktes, das heißt, ein Teil des Trethubes wird nicht in Fahrweg, sondern in Fahrzeuganhebung umgesetzt. Die dafür aufgewendete Energie scheint verloren. Wenn man sich aber vorstellt, daß jetzt das Tretlager blockiert wird, so wird das Absenken des Fahrzeugs in Vorwärtsbewegung umgesetzt. Der eben aufgewendete zusätzliche Weg wird also wieder zurückgewonnen.
Ein anderes Beispiel: Bei einem normalen Fahrrad mit weich gefedertem Sattel federt dieser bei kräftigem Treten zunächst aus. Wenn die Tretkraft dann allmählich nachlässt, federt der Sattel aber bereits wieder ein. am Beginn und am Ende des Hubes z. B. des linken Beins ist der Sattel also eingefedert. Das Bein muß also gar keine Mehrarbeit leisten, sondern der Tretvorgang wird sozusagen nur verzerrt: im Bereich steigender Tretkraft muß der Fuß einen größeren Weg zurücklegen, als es der Vorwärtsbewegung des Rads unter Berücksichtigung der Übersetzung und Kurbellänge entspräche, im Bereich abnehmender Tretkraft dafür einen entsprechen kleineren Weg.
Starkes Arbeiten der Federung ist also vor allem deshalb unerwünscht, weil es einen ungewohnt »eckigen« Tritt ergibt. Außerdem geht der Reibungsanteil der Bewegung in Schwingenlager, Federn und Federaufhängung verloren. Nur ist dieser Anteil eine ganze Größenordnung kleiner, als wir alle gedacht haben.
Nun kann man sich zwar an eine beim starken Treten federnde Hinterradaufhängung gewöhnen, wie ich an meinem »Alfa« festgestellt habe, man gewöhnt sich halt einen »runderen« Tritt an. Der Gewinn an Fahrkomfort wäre das auf jeden Fall wert.
Noch besser aber ist natürlich eine Federung ohne Tretreaktion Zunächst glaubt man, die Welt wäre in Ordnung, wenn der ziehende Kettenstrang exakt durch den Schwingendrehpunkt gehe. Auch hier habe ich wieder von Wilfried gelernt.

An der Schwinge greift nämlich nicht nur der periodisch schwankende Kettenzug FK, sondern als dessen Folge eine im Radaufstandspunkt angreifende ebenfalls periodisch schwankende Beschleunigungskraft F Ban. Außerdem schwanken dadurch auch die Radlasten. Diese 3 Kräfte müssen zusammen betrachtet werden.
Die aus FK, FBund der Radlaständerung FAgebildete Resultierende FRwird in die Radmitte gelegt. Der optimale Drehpunkt der Schwinge liegt dann auf dieser Resultierenden.
Für das Langliegerad ergibt sich als optimaler Schwingendrehpunkt ca. 20–30 mm unter dem ziehenden Kettenstrang. Es bedarf also keiner besonderen Anstrengung, um das ziehende Kettentrum exakt durch den Schwingendrehpunkt zu führen. Bei meinem »Diogenes« hatte ich noch extra ein geteiltes Schwingenlager gebaut (man könnte die Kette auch neben dem Schwingenlager laufen lassen). Es genügt, wenn das obere Kettentrum in der der Nähe, das heißt ca. 20 mm über der Schwingenachse, verläuft. Das Ganze gilt genau nur für das normale Langliegerad ohne Nabenschaltung.
Ein Zwischenrad auf der Schwingenlagerachse eliminiert übrigens das Federn beim Treten nicht von vornherein, gibt aber größere Freiheit in der Anstellung der Schwinge, das heißt man kann die Schwinge steiler oder flacher anstellen, ohne daß es mit der Kettenlinie Probleme gibt.
Dämpfung
Im Gegensatz zur Laienmeinung ist Dämpfung etwas völlig anderes als Federung. Physikalisch gesehen hat Dämpfung immer etwas mit Reibung zu tun, z. B. Lagerreibung, Flüssigkeitsreibung in einem hydraulischen Stoßdämpfer oder innere (Material-)Reibung z. B. in Gummi.
Reibung wirkt sich so aus, daß für das Einfedem größere Kräfte erforderlich sind als für das Ausfedern (siehe Skizze). Die Fläche zwischen den Kennlinien ist Ausdruck für die in Wärme umgewandelte Reibungsenergie. Aus zwei Gründen ist Reibung bzw. Dämpfung an sich unerwünscht.
Erstens geht die in Wärme umgewandelte Reibungsenergie für die Fortbewegung verloren, und wo sollte diese Energie herkommen, als letztlich aus den Muskeln des Fahrers. Außerdem verschlechtert hohe Reibung das Ansprechvermögen der Federung, die Federung reagiert auf kleine Unebenheiten überhaupt nicht mehr. Warum macht man sich dann überhaupt Gedanken über diese unerwünschte Dämpfung?
Stellen wir uns vor, ein Fahrrad mit einer absolut reibungsfreien Federung (die es in der Praxis natürlich nicht gibt) fährt über einen Stein. Dann würde das Rad einfedern und überhaupt nicht mehr aufhören nachzuschwingen. Wenn jetzt noch ein weiterer Stoß dazu käme, könnte es zu unangenehmen Überlagerungen kommen oder der Bodenkontakt geht sogar total verloren.
Eine gewisse Dämpfung ist also erforderlich. Bei Autos, Motorrädern und teureren gefederten Fahrädern haben sich hydraulische Dämpfer als Optimum herausgestellt, die bei starken Stößen stärker dämpfen als bei schwachen und das Ausfedern stärker als das Einfedern.
Für den Bastler ist es leider nicht damit getan, irgendeine Gasdruckfeder eines Kofferraumdeckels oder einen Dämpfer aus einer alten Waschmaschine anzubauen. Diese dämpfen nämlich meist viel zu stark. Die richtige Dämpferabstimmung ist so schwierig, daß nicht einmal alle Autowerke dies heute beherrschen. Für Reifendrücke bis ca 4 bar und Geschwindigkeiten bis etwa 40 km finde ich die Eigendämpfung von Gummi und vor allem von PU-Schaum ausreichend, während sich ungedämpfte Stahlfedern allein gefährlich aufschaukeln können.
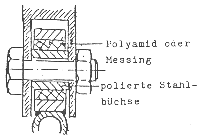
Als Schwingenlager verwende ich meist selbst gedrehte Buchsen aus Polyamid, hinten 20 mm, vorn 12 mm breit, Innendurchmesser hinten 8 mm, als Lagerbolzen dient 8 mm-Silberstahl. Damit sich dieser nicht mitdreht, löte ich auf einer Seite die Mutter auf und hindere diese durch einen kleinen Blechwinkel am Schwingenlagerauge am Drehen.
Vorn lasse ich die Buchse auf einer Stahlhülse, 6 innen, 8 außen, laufen, damit man die Schraube fest anziehen kann. (Die Hülse ist 0,5 mm länger als die Buchse).
Hinten benutze ich das Schwingenrohr als Ölvorratsbehälter (Verschlußbohrung M5 in der Mitte oben). Eine gute Lösung sind auch vorgefertigte Buchsen aus Stahlblech mit einer Beschichtung aus Sinterbronze und Teflon, wie sie in preiswerter Form z. B. die Fa. SKF unter dem Namen Glycodur vertreibt. Auch ein altes Tretlager oder eine (evtl. verbreiterte) Hinterradnabe lassen sich zur Schwingenlagerung mißbrauchen.
Verstellbarkeit
Ein drahtiges Kerlchen wiegt vielleicht 60 kg, ein anderer 85 + 35 kg Gepäck, das heißt die Belastung kann sich um 100 % unterscheiden. Die Federhärte kann also entweder nur ein Kompromiß sein, der dann aber für den leichten Fahrer viel zu hart ist, oder man sieht eine Federverstellung vor.
Die einfachste Möglichkeit ist eine Erhöhung der Vorspannung, z. B. mit einer Stellschraube oder mit Umstecken der Federaufhängung in verschiedene Bohrungen. Besser ist eine Verstellung der Federhärte. Möglich ist z. B. ein zusätzliches Einhängen von Gummiringen oder ein Verschieben des Federangriffspunktes. Äußerst wirksam ist die Längenverstellung einer auf Biegung beanspruchten Blattfeder, weil deren wirksame Länge mit der 4. Potenz in die Federzahl eingeht. Vorn ist eine Verstellung nur erforderlich, wenn dort ein Gepäckträger sitzt.
Rechenbeispiele
Beim Langlieger mit ca 1650 mm Radstand liegen 75 % des Gesamtgewichtes auf dem Hinterrad. Die statische Radlast beträgt also
Aus Radgröße und Rahmengeometrie ergibt sich das Hebelverhältnis der
Schwinge, nehmen wir an, wir hätten
Wir wollen einen guten Fahrkomfort und wählen einen Federweg von 10 cm, dazu kommt noch der statische Federweg. Die Erfahrung zeigt, daß die dynamische Radlast (Stoßbelastung) um das 1,5-fache über der statischen Belastung liegen kann. Die dynamische Belastung beträgt also
Die Federzahl auf die Achse bezogen beträgt also
Diese Federzahl muß noch auf die Feder selbst umgerechnet werden
Verwendet werden sollen Gummiringe von Auspuffaufhängungen mit einer Federzahl von 60 N/cm, erforderlich sind also
Ringe, abgerundet auf 8 (Die Ringe sind z.T. etwas unterschiedlich, ich habe auch schon welche mit 75 N/cm gehabt).
Diese 8 Ringe bringt man normalerweise nicht mehr nebeneinander unter. Ich habe sie einfach in 2 Paketen übereinander angeordnet (parallel).
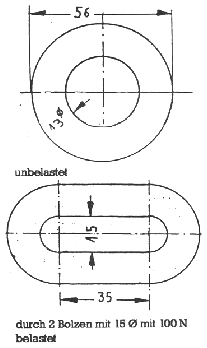
Wenn man PU-Schaum, z. B. Cellasto mit 0,65 g/cm3 verwendet, sieht das wie folgt aus:
Dieser Schaum hat ab etwa 60 % Zusammendrückung eine sehr steile Kennlinie, deshalb soll der Block nur um 50 % gedrückt werden. Nach den Firmenunterlagen gehört zu 50 % Zusammendrückung eine Spannung von 1,6 N/cm2. Die Maximalkraft an der Feder ist 1688 ∙ 2,2 = 3713,6 N. Die erforderliche Fläche ergibt sich zu
Dazu kommen noch für die Bohrung von 12 mm = 113 mm2, ergibt eine Gesamtfläche von 2434 mm2. Daraus errechnet man den Durchmesser des Blocks zu 55 mm.
Bei statischer Belastung ergibt sich aus dieser Fläche und dem gewählten Hebelverhältnis eine Spannung von 0,57 N/mm2. Dazu gehört nach dem Diagramm eine Zusammendrückung von 15 %. Die Wegdifferenz an der Feder zwischen statischer und dynamischer Belastung beträgt 100 ∙ 2,22 = 45 mm. Diese 45 mm entsprechen also einer Zusammendrückung von 50 - 15 = 35 %. Daraus errechnet sich die Länge des PU-Blocks zu 128,5 mm.
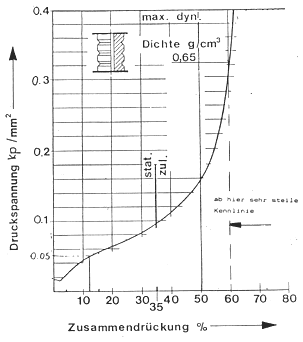
Wenn man umgekehrt einen bestimmten PU-Block hat, kann man dessen Federzahl mit einer kleinen Vorrichtung messen und dann aus dieser Zahl und der an der Achse gewünschten Federzahl das erforderliche Hebelverhältnis ausrechnen.
Beispiel
Der vorhandene Block hätte 400 N/cm, an der Achse will man 100 N/cm haben:
Hebelverhältnis
Rechenbeispiel: Eine Schwinge habe das Hebelverhältnis
Das Hebelverhälmis geht also quadratisch ein.
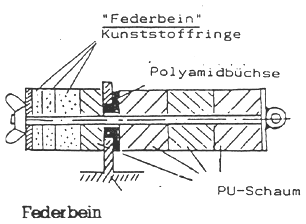
Wenn man Gummi- oder PU-Blöcke verwendet, die mehr als doppelt so lang wie dick sind, muß eine Sicherung gegen Ausknicken da sein, z. B. ein Führungsbolzen, das heißt man baut ein regelrechtes »Federbein«.
Die Aufhängung am Rahmen, die Verbindung zwischen Bolzen und Auge und die Aufhängung an der Schwinge müssen sehr solide sein, da die Federkräfte ca. 3000 N, also 6 Zentner betragen können.
Vorderradfederung
Beim Langliegerad ist eine vordere Federung zwar weniger wichtig als hinten (etwa im Verhältnis der Radlasten 25:75 %), wenn man aber eine Weile mit gut gefedertem Hinterrad gefahren ist, fallen einem allmählich die Stöße am Vorderrad auf.
Eine gute Vorderradfederung soll: 1. ausreichend Federweg haben (ca. 50–70 mm) 2. genügend weich sein (bei etwa 2,5-facher statischer Radlast voll einfedern) 3. wartungs- und spielfreie Lager haben 4. das Rad exakt führen, das heißt seitensteif sein 5. das Rad in der Hauptstoßrichtung einfedern lassen (senkrecht oder leicht schräg nach hinten oben) 6. die Bremskräfte einwandfrei aufnehmen 7. leicht ansprechen, das heißt wenig Reibung haben 8. wenig Mehrgewicht bringen 9. leicht zu bauen sein 10. evtl. auf unterschiedliche Belastungen einstellbar sein.
Die bei Motorrädern vorherrschende Teleskopgabel spricht nur bei sehr sorgfältiger Ausführung leicht an und ist relativ schwer. Die günstigere Ausführung ist meines Erachtens eine geschobene Kurzschwinge mit Versteifungsbügel, Schwingenlänge ca. 80 mm, kürzer gibt kleineren Federweg, länger mindert die Seitensteifigkeit. Gezogene Schwingen scheinen noch leichter anzusprechen, haben aber den Nachteil, daß sie beim Bremsen voll in die Knie gehen.
Eine geschobene Schwinge dagegen stellt sich beim Bremsen (vorne) auf. Um dieses Aufstellen in Grenzen zu halten, sollte man die Federn so vorspannen, daß der Ausfederweg bei belastetem Rad nur 1–2 cm beträgt. Außerdem sollte als oberer Anschlag ein Gummipuffer da sein, um den metallischen Schlag zu vermeiden. Auch das Einfedern sollte durch einen Puffer begrenzt werden, um Durchschlagen zu vermeiden und zur Sicherheit bei Federbruch.
Als Federelemente kommen auch hier PU- oder Gummiblöcke, Gummiringe und Schraubenfedern (Zug oder Druck) in Frage. Noch einmal: Bei der Konzeption der Federung ist zu bedenken, daß der Hebelarm der Feder quadratisch in die Härte der Federung eingeht!
Bei der Vorderradfederung lässt sich leichtes Federn beim Treten nicht durch geometrische Tricks vermeiden. Wen das stört, der sollte die Vorderfederung eher etwas härter abstimmen.
Federung beim Kurzliegerad
Beim Kurzliegerad gibt es meist keine Achse, die den größten Teil der Last aufnimmt und dadurch eine Federung schon dieser Achse einen so eindrucksvollen Erfolg bringt wie beim Langliegerad (70–80 % auf dem Hinterrad). Man wird also wohl beide Räder federn müssen. Sonst gilt alles oben Gesagte.
Verschiedene Ausführungen für gefederte Vordergabeln

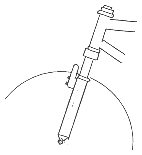
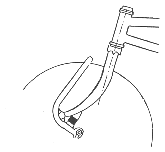
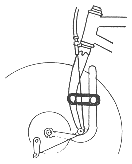
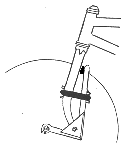
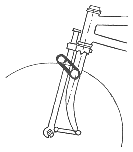
Anbau jeder Bremse möglich, ähnlich Moulton
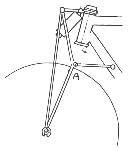
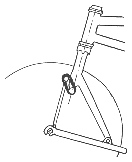
üppiger Federweg, steife Konstruktion erforderlich
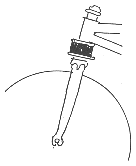
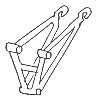
einfach zu bauen, Spielfreiheit sehr wichtig Beispiele für die Federung des Hinterrades
Beispiele für die Federung des Hinterrades
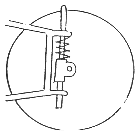
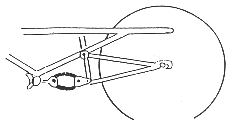
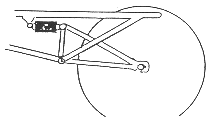
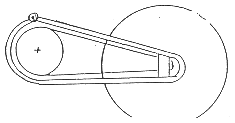

Zum Autor
 Werner Stiffel, Jahrgang 35, Karlsruhe, beschloss 1990 das Liegerad zu verbessern,
gab seinen Beruf auf, sammelte jede erreichbare Information zu diesem
Thema, konstruierte, baute und erprobte ungefähr 100 verschiedene
Liegeräder mit 2, 3 oder 4 Rädern.
Werner Stiffel, Jahrgang 35, Karlsruhe, beschloss 1990 das Liegerad zu verbessern,
gab seinen Beruf auf, sammelte jede erreichbare Information zu diesem
Thema, konstruierte, baute und erprobte ungefähr 100 verschiedene
Liegeräder mit 2, 3 oder 4 Rädern.